一、RBF神经网络

1. RBF神经网络概述
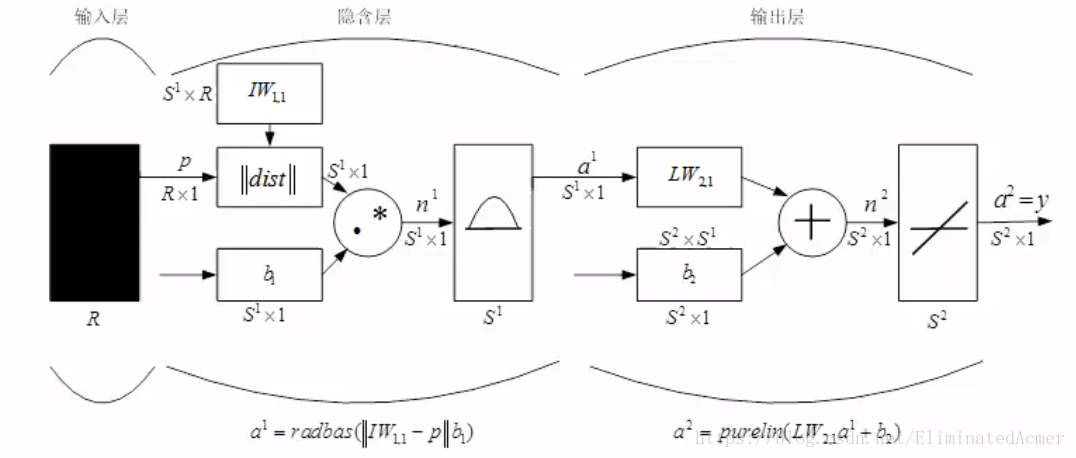
   • 径向基函数神经网络
   • 与 BP 神经网络的区别在于训练过程——其参数初始化具有一定方法，并非随机，隐含层的末尾使用了径向基函数，它的输出经过加权和得到 LW2.1LW2.1

1. RBF神经网络重点函数介绍

   • newrbe()——创建精确的径向基网络
     • net = newrbe(P , T , Spread)
     • P: 输入向量
     • T：输出向量
     • Spread：径向基的扩展速度

2. RBF代码使用实例

%% I. 清空环境变量

clear all

clc

%% II. 训练集/测试集产生

%%

% 1. 导入数据

load spectra_data.mat

%%

% 2. 随机产生训练集和测试集

temp = randperm(size(NIR,1));

% 训练集——50个样本

P_train = NIR(temp(1:50),:)’;

T_train = octane(temp(1:50),:)’;

% 测试集——10个样本

P_test = NIR(temp(51:end),:)’;

T_test = octane(temp(51:end),:)’;

N = size(P_test,2);

%% III. RBF神经网络创建及仿真测试

%%

% 1. 创建网络

net = newrbe(P_train,T_train,30);

%%

% 2. 仿真测试

T_sim = sim(net,P_test);

%% IV. 性能评价

%%

% 1. 相对误差error

error = abs(T_sim - T_test)./T_test;

%%

% 2. 决定系数R^2

R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));

%%

% 3. 结果对比

result = [T_test’ T_sim’ error’]

%% V. 绘图

figure

plot(1:N,T_test,’b:*’,1:N,T_sim,’r-o’)

legend(‘真实值’,’预测值’)

xlabel(‘预测样本’)

ylabel(‘辛烷值’)

string = {‘测试集辛烷值含量预测结果对比’;[‘R^2=’ num2str(R2)]};

title(string)

二、GRNN、PNN神经网络

1. GRNN神经网络概述

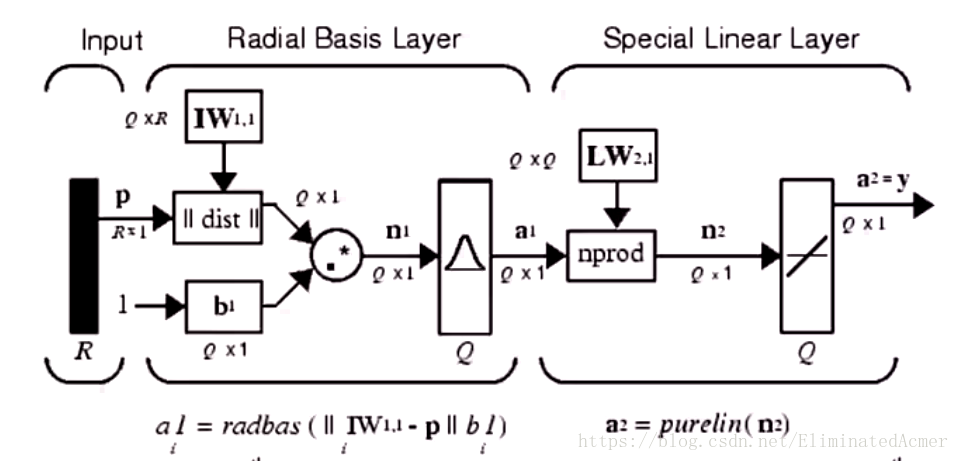
   • 广义回归神经网络

   • 输入层和隐含层与 RBF 神经网络一致，这里的 LW2.1LW2.1 直接由输出矩阵代替，并在隐含层与输出层之间和激活函数进行点乘

1. PNN神经网络概述

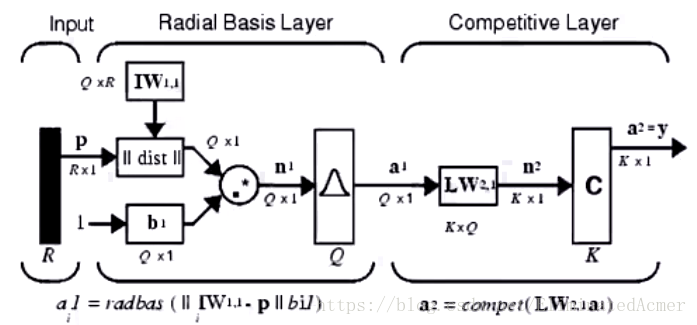
   • 概率神经网络

   • 输入层和隐含层与RBF神经网络一致，不同点是最后的输出环节使用了一个竞争函数

1. GRNN、PNN神经网络重点函数介绍

   • newgrnn()——创建广义回归神经网络
     • net = newgrnn(P,T)
     • P，T 和RBF神经网络一致
   • newpnn()——创建概率神经网络
     • net = newpnn(P,T)
     • P，T 同上

2. 代码使用实例

%% I. 清空环境变量

clear all

clc

%% II. 训练集/测试集产生

%%

% 1. 导入数据

load iris_data.mat

%%

% 2 随机产生训练集和测试集

P_train = [];

T_train = [];

P_test = [];

T_test = [];

for i = 1:3

temp_input = features((i-1)*50+1:i*50,:);

temp_output = classes((i-1)*50+1:i*50,:);

n = randperm(50);

% 训练集——120个样本

P_train = [P_train temp_input(n(1:40),:)’];

T_train = [T_train temp_output(n(1:40),:)’];

% 测试集——30个样本

P_test = [P_test temp_input(n(41:50),:)’];

T_test = [T_test temp_output(n(41:50),:)’];

end

%% III. 模型建立

result_grnn = [];

result_pnn = [];

time_grnn = [];

time_pnn = [];

for i = 1:4

for j = i:4

p_train = P_train(i:j,:);

p_test = P_test(i:j,:);

%%

% 1. GRNN创建及仿真测试

t = cputime;

% 创建网络

net_grnn = newgrnn(p_train,T_train);

% 仿真测试

t_sim_grnn = sim(net_grnn,p_test);

T_sim_grnn = round(t_sim_grnn);

t = cputime - t;

time_grnn = [time_grnn t];

result_grnn = [result_grnn T_sim_grnn’];

%%

% 2. PNN创建及仿真测试

t = cputime;

Tc_train = ind2vec(T_train);

% 创建网络

net_pnn = newpnn(p_train,Tc_train);

% 仿真测试

Tc_test = ind2vec(T_test);

t_sim_pnn = sim(net_pnn,p_test);

T_sim_pnn = vec2ind(t_sim_pnn);

t = cputime - t;

time_pnn = [time_pnn t];

result_pnn = [result_pnn T_sim_pnn’];

end

end

%% IV. 性能评价

%%

% 1. 正确率accuracy

accuracy_grnn = [];

accuracy_pnn = [];

time = [];

for i = 1:10

accuracy_1 = length(find(result_grnn(:,i) == T_test’))/length(T_test);

accuracy_2 = length(find(result_pnn(:,i) == T_test’))/length(T_test);

accuracy_grnn = [accuracy_grnn accuracy_1];

accuracy_pnn = [accuracy_pnn accuracy_2];

end

%%

% 2. 结果对比

result = [T_test’ result_grnn result_pnn]

accuracy = [accuracy_grnn;accuracy_pnn]

time = [time_grnn;time_pnn]

%% V. 绘图

figure(1)

plot(1:30,T_test,’bo’,1:30,result_grnn(:,4),’r-*’,1:30,result_pnn(:,4),’k:^’)

grid on

xlabel(‘测试集样本编号’)

ylabel(‘测试集样本类别’)

string = {‘测试集预测结果对比(GRNN vs PNN)’;[‘正确率:’ num2str(accuracy_grnn(4)*100) ‘%(GRNN) vs ’ num2str(accuracy_pnn(4)*100) ‘%(PNN)’]};

title(string)

legend(‘真实值’,’GRNN预测值’,’PNN预测值’)